Comment faire un test T dans Excel

Comment faire un test T dans Excel

Un test t est une méthode qui utilise la distribution t de Student pour déterminer s’il existe une différence statistiquement significative entre les ensembles de données. Un test T dans Excel est un test T à deux échantillons qui compare les moyennes de deux échantillons. Cet article explique ce que signifie la signification statistique et montre comment effectuer un test T dans Excel.

Les instructions de cet article s’appliquent à Excel 2019, 2016, 2013, 2010, 2007 ; Excel pour Microsoft 365 et Excel Online.

Crédit image, Getty Images

Qu’est-ce que la signification statistique ?

Imaginez que vous vouliez savoir lequel des deux dés donnera le meilleur score. Vous lancez le premier dé et obtenez un 2 ; vous lancez le deuxième dé et obtenez un 6. Cela vous indique-t-il que le deuxième dé donne généralement un score plus élevé ? Si vous avez répondu « bien sûr que non », alors vous savez déjà quelque chose sur la signification statistique. Vous savez que la différence est due à des changements aléatoires dans le score à chaque fois que les dés sont lancés. Parce que l’échantillon est très petit (un seul volume), il ne montre rien de significatif.

Imaginez maintenant que vous lancez chaque dé 6 fois :

• 1er jet de dé 3, 6, 6, 4, 3, 3 ; Moyenne = 4,17
• 2e jet de dé 5, 6, 2, 5, 2, 4 ; moyenne = 4,00

Cela prouve-t-il que le score du premier dé est supérieur au second ? peut être pas. Le petit échantillon avec des différences relativement faibles entre les moyennes rend la différence probablement encore due à une variation aléatoire. Au fur et à mesure que nous augmentons le nombre de lancers de dés, il devient difficile de donner une réponse de bon sens à la question – la différence entre les scores est-elle le résultat d’une variation aléatoire, ou est-elle en fait plus susceptible de donner un score plus élevé que l’autre ?

La signification est la probabilité que la différence observée entre les échantillons soit due à une variation aléatoire. L’importance est souvent appelée niveau alpha ou simplement « alpha ». Le niveau de confiance, ou « c » en abrégé, est la probabilité que la différence entre les échantillons ne soit pas due à une variation aléatoire ; en d’autres termes, il existe une différence entre les populations sous-jacentes. alors: C = 1 – alpha

Nous pouvons définir « alpha » à n’importe quel niveau que nous voulons pour être sûr que nous avons démontré l’importance. α = 5 % (niveau de confiance de 95 %) est souvent utilisé, mais si nous voulons être vraiment sûrs que les différences ne sont pas dues à une variation aléatoire, nous pouvons appliquer un niveau de confiance plus élevé, en utilisant α = 1 % ou même α = 0,1 %.

Divers tests statistiques sont utilisés pour calculer la signification dans différentes situations. Le test T est utilisé pour déterminer si les moyennes de deux populations sont différentes, et le test F est utilisé pour déterminer si les variances sont différentes.

Pourquoi tester la signification statistique ?

Lorsque nous comparons différentes choses, nous devons utiliser un test de signification pour déterminer si l’une est meilleure que l’autre. Cela s’applique à de nombreux domaines tels que :

• En affaires, il faut comparer différents produits et méthodes de commercialisation.
• Dans le sport, il faut comparer différents équipements, technologies et concurrents.
• En ingénierie, il faut comparer différentes conceptions et réglages de paramètres.

Si vous voulez tester si quelque chose fonctionne mieux qu’un autre, dans n’importe quel domaine, vous devez tester la signification statistique.

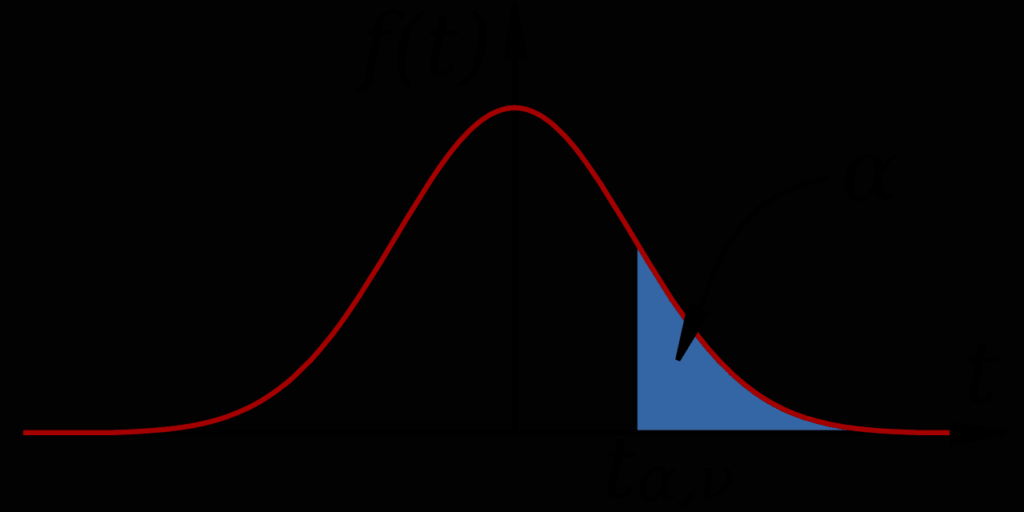
Qu’est-ce que la distribution T de Student ?

La distribution t de Student est similaire à la distribution normale (ou gaussienne). Ce sont des distributions en forme de cloche, avec la plupart des résultats proches de la moyenne, mais quelques événements rares qui sont loin de la moyenne dans les deux sens, appelés les queues de la distribution.

La forme exacte de la distribution t de Student dépend de la taille de l’échantillon. Pour les échantillons de plus de 30, cela ressemble beaucoup à une distribution normale. À mesure que la taille de l’échantillon diminue, les queues s’agrandissent, ce qui indique l’augmentation de l’incertitude causée par les inférences basées sur de petits échantillons.

Comment faire un test T dans Excel

Avant de pouvoir appliquer un test T pour déterminer s’il existe une différence statistiquement significative entre les moyennes de deux échantillons, vous devez d’abord effectuer un test F. En effet, le test T est calculé différemment selon qu’il existe ou non une différence significative entre les variances.

Tu auras besoin de Plug-in de la boîte à outils d’analyse pouvoir effectuer cette analyse.

Inspecter et charger les plugins ToolPak d’analyse

Pour vérifier et activer l’Analysis ToolPak, procédez comme suit :

1. choisir document onglet > sélectionner Choix.

2. Dans la boîte de dialogue Options, sélectionnez Modules complémentaires Onglets à partir de la gauche.

3. En bas de la fenêtre, sélectionnez Gérer menu déroulant et sélectionnez Complément Excel. choisir aller.

4. Assurez-vous que la case à côté de Boîte à outils d’analyse est sélectionné, puis sélectionnez D’ACCORD.

5. La boîte à outils d’analyse est maintenant active et vous pouvez appliquer des tests F et des tests T.

Effectuer F-Test et T-Test dans Excel

1. Entrez les deux ensembles de données dans la feuille de calcul. Dans ce cas, nous envisageons les ventes des deux produits en une semaine. Les ventes quotidiennes moyennes pour chaque produit et son écart-type ont également été calculés.

2. choisir Les données Balises > l’analyse des données

3. choisir Test F de variance pour deux échantillons dans la liste, puis sélectionnez D’ACCORD.

   Le test F est très sensible à la non-normalité. Il est donc probablement plus sûr d’utiliser le test de Welch, mais c’est plus difficile dans Excel.

4. sélectionner la portée de la variable 1 et la portée de la variable 2 ; définir alpha (0,05 donne une confiance de 95 % ); sélectionnez une cellule pour le coin supérieur gauche de la sortie, en considérant que cela remplira 3 colonnes et 10 lignes.choisir D’ACCORD.

   Pour la plage de la variable 1, l’échantillon présentant le plus grand écart type (ou variance) doit être sélectionné.

5. Examinez les résultats du test F pour déterminer s’il existe une différence significative entre les variances. Le résultat donne trois valeurs importantes :

   • F: Le rapport entre les variances.
   • P(F<=f) simple queue: la probabilité que la variable 1 n’ait pas réellement une plus grande variance que la variable 2. Si celui-ci est supérieur à alpha, généralement 0,05, il n’y a pas de différence significative entre les variances.
   • Fin critique F: La valeur de F requise pour donner P(F<=f)=α. Si la valeur est supérieure à F, cela indique également qu'il n'y a pas de différence significative entre les variances.

   P(F<=f) peut également être calculé à l'aide de la fonction FDIST, avec F et les degrés de liberté pour chaque échantillon comme entrées. Les degrés de liberté sont simplement le nombre d'observations dans l'échantillon moins une.

6. Maintenant que vous savez s’il existe une différence entre les variances, vous pouvez choisir un test t approprié.choisir Les données Balises > l’analyse des donnéespuis sélectionnez Test t : deux échantillons en supposant des variances égales ou Test t : deux échantillons avec des variances inégales supposées.

7. Quelle que soit l’option que vous avez sélectionnée à l’étape précédente, vous verrez la même boîte de dialogue pour entrer les détails de l’analyse.Tout d’abord, sélectionnez la plage qui contient l’échantillon portée variable1 et plage variable 2.

8. En supposant que vous vouliez tester qu’il n’y a pas de différence entre les moyennes, définissez Différence moyenne hypothétique zéro.

9. Définissez le niveau de signification Alpha (0,05 donne une confiance de 95 %) et sélectionnez une cellule pour le coin supérieur gauche de la sortie, en considérant que cela remplira 3 colonnes et 14 lignes.choisir D’ACCORD.

10. Examinez les résultats pour déterminer s’il existe une différence significative entre les moyennes.

    Tout comme le test F, si la valeur de p (P(T<=t) dans ce cas) est supérieure à alpha, il n'y a pas de différence significative. Cependant, dans ce cas, deux valeurs de p sont données, une pour le test unilatéral et l'autre pour le test bilatéral. Dans ce cas, utilisez des valeurs bilatérales car toute variable avec une moyenne plus grande sera significativement différente.

Merci de nous en informer!

Recevez les dernières nouvelles technologiques publiées quotidiennement

abonnement

Dites-nous pourquoi !

D’autres détails ne sont pas assez difficiles à comprendre